LeetCode第22次双周赛。前两题比较基础,所以就不记录了。
1 将整数按权重排序
-
题目描述
我们将整数 x 的 权重 定义为按照下述规则将 x 变成 1 所需要的步数:
如果 x 是偶数,那么 x = x / 2 如果 x 是奇数,那么 x = 3 * x + 1 比方说,x=3 的权重为 7 。因为 3 需要 7 步变成 1 (3 –> 10 –> 5 –> 16 –> 8 –> 4 –> 2 –> 1)。
给你三个整数 lo, hi 和 k 。你的任务是将区间 [lo, hi] 之间的整数按照它们的权重 升序排序 ,如果大于等于 2 个整数有 相同 的权重,那么按照数字自身的数值 升序排序 。
请你返回区间 [lo, hi] 之间的整数按权重排序后的第 k 个数。
注意,题目保证对于任意整数 x (lo <= x <= hi) ,它变成 1 所需要的步数是一个 32 位有符号整数。
示例 1:
输入:lo = 12, hi = 15, k = 2 输出:13 解释:12 的权重为 9(12 –> 6 –> 3 –> 10 –> 5 –> 16 –> 8 –> 4 –> 2 –> 1) 13 的权重为 9 14 的权重为 17 15 的权重为 17 区间内的数按权重排序以后的结果为 [12,13,14,15] 。对于 k = 2 ,答案是第二个整数也就是 13 。 注意,12 和 13 有相同的权重,所以我们按照它们本身升序排序。14 和 15 同理。
-
思路分析
- 对于每个数,我们求出它的权重,然后将所有数按照权重排序,取第k大的数。
- 但是在求每个数的权重过程中会有很多重复的情况。比如求3的权重时,会经历3->10->5->16->8->4->2->1。在此过程中我们已经求出了10、5、16、8、4、2的权重,因此,我们将已经求出权重的数字及其权重用hashmap保存。
-
Java代码
class Solution { // map用来记录每个数的权重 Map<Integer, Integer> map = new HashMap<>(); { map.put(1, 0); } public int getKth(int lo, int hi, int k) { // arr[i][0]表示第i个数的值,arr[i][1]表示第i个数的权重 int[][] arr = new int[hi - lo + 1][2]; // 遍历lo到hi,求出所有权重。 for (int i = lo; i <= hi; ++i) { arr[i - lo][0] = i; arr[i - lo][1] = getW(i); } // 按照权重排序,这里也可以用堆,但是题目指出数字不超过1000个,直接排序也可以接受 Arrays.sort(arr, (int[] a1, int[] a2) -> { return a1[1] - a2[1]; }); return arr[k - 1][0]; } // 找到n的权值 public int getW(int n) { if (map.containsKey(n)) { return map.get(n); } if (n % 2 == 0) { int ret = getW(n / 2) + 1; map.put(n, ret); return ret; } else { int ret = getW(3 * n + 1) + 1; map.put(n, ret); return ret; } } }
2 3n 块披萨
-
题目描述
给你一个披萨,它由 3n 块不同大小的部分组成,现在你和你的朋友们需要按照如下规则来分披萨:
你挑选 任意 一块披萨。 Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。 Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。 重复上述过程直到没有披萨剩下。 每一块披萨的大小按顺时针方向由循环数组 slices 表示。
请你返回你可以获得的披萨大小总和的最大值。
示例 1:
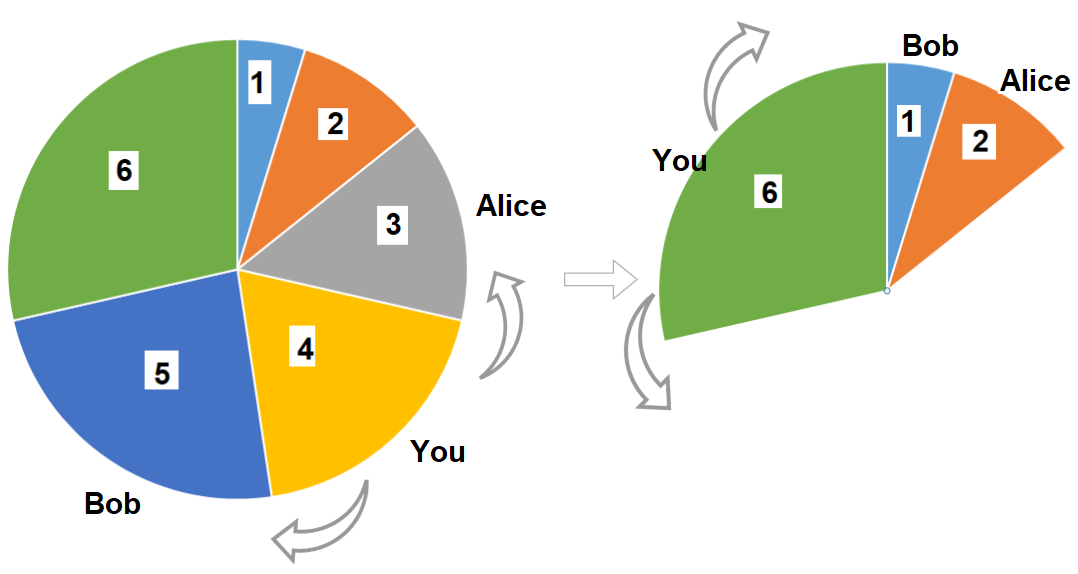
输入:slices = [1,2,3,4,5,6] 输出:10 解释:选择大小为 4 的披萨,Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨,Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。
-
思路分析
-
题目中指出slices.length % 3 == 0,因此我们一定可以拿到slices.length / 3块披萨。
-
我们不能拿相邻的两块披萨。
-
问题转化为:在n块披萨中取n / 3块,使和最大,不能取相邻的披萨。
-
可以使用dp来做,dp[i][j][s]表示,前i块披萨取中取j块能取得的最大值,s表示第i块披萨取还是不取,1表示取。
-
对于第i块披萨,如果要,那么前i块披萨取j块的最大值,就是第i块披萨的值,加上前i-1块披萨,取j-1块,第i-1块不要的最大值。
dp[i][j][1] = dp[i-1][j-1][0] + slices[i]
-
对于第i块披萨,如果不要,那么前i块披萨取j块的最大值,dp[i-1][j][0]和dp[i-1][j][1]中的较大值。
dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1])
-
由于数组呈环形,所以在处理最后一块披萨时需要考虑第一块披萨要没要,但这时根据倒数第二块披萨已经无从考据第一块披萨是否要了。因此可以将dp分为第一块要和不要两种情况进行。
-
-
Java代码
class Solution { public int maxSizeSlices(int[] slices) { int length = slices.length; int picks = length / 3; // dp[i][j][s] 表示前i块披萨,拿了j块,最大值是多少,s表示第i块披萨是要还是不要 int[][][] dp = new int[length][picks + 1][2]; // 分第一块要和第一块不要两种情况 int result = 0; // 第一块要 dp[0][1][1] = slices[0]; for (int i = 1; i < length; ++i) { if (i == length - 1) { // 对于最后一块pisa // 第一块要了,那么它必须不能要 continue; } for (int j = 1; j <= picks; ++j) { // 对于第二块,只能选择不要 if (i == 1) { dp[i][j][0] = dp[i - 1][j][1]; continue; } // 对于第i块披萨,如果要,那么最大值为i-1不要,拿了j-1块 dp[i][j][1] = dp[i - 1][j - 1][0] + slices[i]; // 如果不要,那么最大值为i-1不要,拿了j块,或i-1要,拿了j块 dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1]); } result = Math.max(result, Math.max(dp[i][picks][1], dp[i][picks][0])); } // 第一块不要 dp[0][1][1] = 0; // 第二块可以要,也可以不要,所以不需要特殊处理 for (int i = 1; i < length; ++i) { for (int j = 1; j <= picks; ++j) { // 对于第i块披萨,如果要,那么最大值为i-1不要,拿了j-1块 dp[i][j][1] = dp[i - 1][j - 1][0] + slices[i]; // 如果不要,那么最大值为i-1不要,拿了j块,或i-1要,拿了j块 dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1]); } result = Math.max(result, Math.max(dp[i][picks][1], dp[i][picks][0])); } return result; } }