Gear with Code Java Engineer

LeetCode第180次周赛题。

2020-03-15
算法

LeetCode第180次周赛题。

1 矩阵中的幸运数

  1. 题目描述

    给你一个 m * n 的矩阵，矩阵中的数字 各不相同 。请你按 任意 顺序返回矩阵中的所有幸运数。

    幸运数是指矩阵中满足同时下列两个条件的元素：

    • 在同一行的所有元素中最小
    • 在同一列的所有元素中最大

    示例 1：

    输入：matrix = [[3,7,8],[9,11,13],[15,16,17]]
输出：[15]
解释：15 是唯一的幸运数，因为它是其所在行中的最小值，也是所在列中的最大值。

  2. 思路分析

    • 遍历每一行，先找出它的最小值。
    • 再遍历最小值所在这一列，如果不存在任何值比它大，那么这就是一个幸运数。

  3. Java代码

    class Solution {
    public List<Integer> luckyNumbers (int[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) {
            return new ArrayList<Integer>();
        }
           
        int rows = matrix.length;
        int cols = matrix[0].length;
           
        List<Integer> result = new ArrayList<Integer>();
           
        for (int i = 0; i < rows; ++i) {
            int minIndex = 0;
            for (int j = 1; j < cols; ++j) {
                if (matrix[i][j] < matrix[i][minIndex]) {
                    minIndex = j;
                }
            }
               
            boolean flag = true;
            for (int k = 0; k < rows; ++k) {
                if (matrix[k][minIndex] > matrix[i][minIndex]) {
                    flag = false;
                    break;
                }
            }
               
            if (flag) {
                result.add(matrix[i][minIndex]);
            }
        }
           
        return result;
    }
}

2 设计一个支持增量操作的栈

  1. 题目描述

    请你设计一个支持下述操作的栈。

    实现自定义栈类 CustomStack ：

    • CustomStack(int maxSize)：用 maxSize 初始化对象，maxSize 是栈中最多能容纳的元素数量，栈在增长到 maxSize 之后则不支持 push 操作。
    • void push(int x)：如果栈还未增长到 maxSize ，就将 x 添加到栈顶。
    • int pop()：返回栈顶的值，或栈为空时返回 -1 。
    • void inc(int k, int val)：栈底的 k 个元素的值都增加 val 。如果栈中元素总数小于 k ，则栈中的所有元素都增加 val 。

  2. 思路分析

    不说了，这题直接上代码吧。

  3. Java代码

    class CustomStack {
    int maxSize = 0;
    int size = 0;
       
    int[] stack;
   
    public CustomStack(int maxSize) {
        this.maxSize = maxSize;
        stack = new int[maxSize];
    }
       
    public void push(int x) {
        if (size == maxSize) {
            return;
        }
        stack[size] = x;
        ++size;
    }
       
    public int pop() {
        if (size == 0) {
            return -1;
        }
        int result = stack[size - 1];
        --size;
        return result;
    }
       
    public void increment(int k, int val) {
        for (int i = 0; i < k && i < size; ++i) {
            stack[i] += val;
        }
    }
}

3 将二叉搜索树变平衡

  1. 题目描述

    给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。

    如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

    如果有多种构造方法，请你返回任意一种。

    img

    img

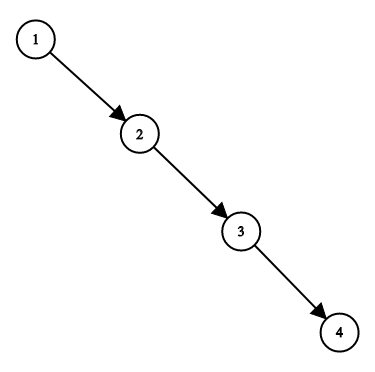
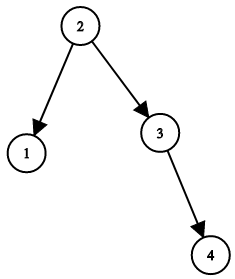
  2. 思路分析

    • 中序遍历将所有节点放到数组中。
    • 采用分治法，取中点作为根节点，递归恢复左子树和右子树。

  3. Java代码

    class Solution {
    List<TreeNode> list = new ArrayList<>();
    public TreeNode balanceBST(TreeNode root) {
        if (root == null) {
            return null;
        }
           
        bstToList(root);
        return rebuild(list, 0, list.size() - 1);
    }
       
    // 重建二叉搜索树
    public TreeNode rebuild(List<TreeNode> list, int left, int right) {
        if (left > right) {
            return null;
        }
        if (left == right) {
            return list.get(left);
        }
           
        int mid = (left + right) / 2;
        TreeNode root = list.get(mid);
        root.left = rebuild(list, left, mid - 1);
        root.right = rebuild(list, mid + 1, right);
        return root;
    }
       
    // 中序遍历保存到数组
    public void bstToList(TreeNode root) {
        if (root == null) {
            return;
        }
           
        bstToList(root.left);
        list.add(root);
        bstToList(root.right);
        root.left = null;
        root.right = null;
    }
}

4 最大的团队表现值

  1. 题目描述

    公司有编号为 1 到 n 的 n 个工程师，给你两个数组 speed 和 efficiency ，其中 speed[i] 和 efficiency[i] 分别代表第 i 位工程师的速度和效率。请你返回由最多 k 个工程师组成的 最大团队表现值 ，由于答案可能很大，请你返回结果对 10^9 + 7 取余后的结果。

    团队表现值 的定义为：一个团队中「所有工程师速度的和」乘以他们「效率值中的最小值」。

    示例 1：

    输入：n = 6, speed = [2,10,3,1,5,8], efficiency = [5,4,3,9,7,2], k = 2
输出：60
解释：
我们选择工程师 2（speed=10 且 efficiency=4）和工程师 5（speed=5 且 efficiency=7）。他们的团队表现值为 performance = (10 + 5) * min(4, 7) = 60 。

  2. 思路分析

    • 团队的最大表现值实际上取决于最小的efficiency是多少，可以将问题转化为：对每一个工程师，如果他的effiency是团队的最小值，我们在所有efficiency大于等于他的工程师中，选择k个，使speed的和最大。也就是说，我们要遍历efficiency数组，然后对每一个efficiency找出所有比它大的，然后在对应的speed中选取k个最大的。
    • 为了对每一个efficiency我们能够快速的找到所有大于它的efficiency，我们先将所有工程师按照efficiency排序，对于efficiency相同的，当然是按照speed排序。排序后，对数组中的每一个元素来说，其后面的所有元素就都是efficiency比它大的。
    • 接下来的问题是，如何快速找到这些元素中，speed前k大的。这就是经典的求前k大的问题。我们可以从后向前遍历数组，然后使用小顶堆，维持小顶堆的元素数为k个。
    • 还有一个问题是，题目要求最多k个，也就是少于k个也可以。实际上，我们在从后向前遍历时，从第一个开始就可以计算团队表现值，而不必等到k个。
    • 这是因为这样一个事实：如果选取p（p<k）个工程师就能取到最大团队表现值，那么这p个工程师一定是efficiency前p大的工程师，也就是我们排序数组的后p个元素。
    • 可以用反证法证明，假设有p（p<k）个工程师组成的团队表现值最大，并且这p个工程师的efficiency不是所有工程师中前p，这p个中的最小值为pmin，那么必然存在这p个之外的工程师的efficiency>=pmin，我们将这个工程师也加入到团队中，此时p+1<=k，efficiency的最小值仍然是pmin，这是团队表现值一定会增加，就与我们的假设矛盾。

  3. Java代码

    class Solution {
    public int maxPerformance(int n, int[] speed, int[] efficiency, int k) {
        // 将speed和efficiency放到一个二维数组中，每一行表示一个工程师
        // 第一列表示speed
        // 第二列表示efficiency
        int[][] arr = new int[n][2];
        for (int i = 0; i < n; ++i) {
            arr[i][0] = speed[i];
            arr[i][1] = efficiency[i];
        }
   
        // 将二维数组排序
        Arrays.sort(arr, (int[] e1, int[] e2)->{
            // efficiency值相等的按照speed排序
            if (e1[1] == e2[1]) {
                return e1[0] - e2[0];
            } else {
                // 否则按照efficiency排序
                return e1[1] - e2[1];
            }
        });
   
        // 用一个小顶堆保存前k大的速度
        long sum = 0; // 记录前k大的speed之和
        long result = 0; // 记录最大团队表现值
        PriorityQueue<Integer> heap = new PriorityQueue<Integer>();
        // 从大到小遍历效率
        for (int i = n - 1; i >= 0; --i) {
            // 如果堆已满k个
            if (heap.size() == k) {
                // 如果当前速度大于堆顶，那么弹出堆顶，放入当前速度
                if (arr[i][0] > heap.peek()) {
                    int top = heap.remove();
                    heap.add(arr[i][0]);
                    sum -= top;
                    sum += arr[i][0];
                       
                    result = Math.max(result, sum * arr[i][1]);
                } else {
                    // 否则啥也不做
                }
            } else {
                // 如果未满k个，直接放入
                heap.add(arr[i][0]);
                sum += arr[i][0];
                   
                result = Math.max(result, sum * arr[i][1]);
            }
        }
   
        return (int)(result % 1000000007);
    }
}

Similar Posts

上一篇 如何给女朋友解释BIO-NIO-AIO

下一篇 读书笔记-Redis哨兵

Comments

Content