LeetCode第179次周赛题。
1 生成每种字符都是奇数个的字符串
-
题目描述
给你一个整数 n,请你返回一个含 n 个字符的字符串,其中每种字符在该字符串中都恰好出现 奇数次 。
返回的字符串必须只含小写英文字母。如果存在多个满足题目要求的字符串,则返回其中任意一个即可。
示例 1:
输入:n = 4 输出:”pppz” 解释:”pppz” 是一个满足题目要求的字符串,因为 ‘p’ 出现 3 次,且 ‘z’ 出现 1 次。当然,还有很多其他字符串也满足题目要求,比如:”ohhh” 和 “love”。
-
思路
如果n是奇数就生成n个’a’,否则,生成1个’a’和n-1个’b’。
-
C++代码
class Solution { public: string generateTheString(int n) { if (n == 0) { return string(); } if (n % 2 == 1) { return string(n, 'a'); } else { return string(1, 'a') + string(n - 1, 'b'); } } };
2 灯泡开关 III
-
题目描述
房间中有 n 枚灯泡,编号从 1 到 n,自左向右排成一排。最初,所有的灯都是关着的。
在 k 时刻( k 的取值范围是 0 到 n - 1),我们打开 light[k] 这个灯。
灯的颜色要想 变成蓝色 就必须同时满足下面两个条件:
灯处于打开状态。 排在它之前(左侧)的所有灯也都处于打开状态。 请返回能够让 所有开着的 灯都 变成蓝色 的时刻 数目 。
示例1:
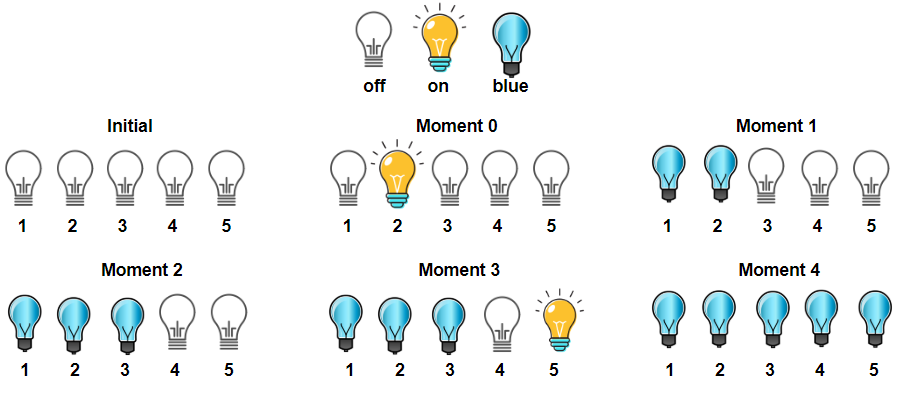
输入:light = [2,1,3,5,4] 输出:3 解释:所有开着的灯都变蓝的时刻分别是 1,2 和 4 。
-
思路分析
- 用一个新的数组记录每个灯的颜色,0不亮,1黄色,2蓝色。
- 按照电灯顺序依次电灯。
- 若点的灯是第一个灯,直接点为蓝色。
- 若点的灯不是第一个灯,判断它前面灯的颜色。若是蓝色,则此灯点为蓝色。若不是,则此灯点为黄色。
- 每点亮一个蓝色的灯,判断它右边的灯是否是黄色,如果是,则点为蓝色。
- 记录点亮的所有的灯中最大的编号。每次点灯时,若点亮的最后一个灯是蓝色,判断此灯是否是最大编号,若是,结果+1;
-
java代码
class Solution { public int numTimesAllBlue(int[] light) { if (light == null || light.length == 0) { return 0; } int length = light.length; int[] color = new int[length]; int result = 0; int maxLight = 0; for (int i = 0; i < length; ++i) { // 如果打开的是第0个灯 if (light[i] - 1 == 0) { // 直接变成蓝色 color[0] = 2; // 如果这是亮着的最右边的灯 if (0 == maxLight) { ++result; } else { // 将它右边的连续的亮着的灯都变成蓝色 int j = 1; for (; j <= maxLight; ++j) { if (color[j] == 1) { color[j] = 2; } else { break; } } if (j == maxLight + 1) { ++result; } } } else { // 如果当前灯前面的灯是蓝色,则变为蓝色 if (color[light[i] - 2] == 2) { color[light[i] - 1] = 2; // 如果此灯是最右边的灯 if (light[i] - 1 >= maxLight) { ++result; maxLight= light[i] - 1; } else { // 将右边亮着的连续的灯变为蓝色 int j = light[i]; for (; j <= maxLight; ++j) { if (color[j] == 1) { color[j] = 2; } else { break; } } if (j == maxLight + 1) { ++result; } } } else { // 前面的灯不是蓝色,点亮此灯 color[light[i] - 1] = 1; maxLight = maxLight > light[i] - 1 ? maxLight : light[i] - 1; } } } return result; } }
3 通知所有员工所需的时间
-
题目描述
公司里有 n 名员工,每个员工的 ID 都是独一无二的,编号从 0 到 n - 1。公司的总负责人通过 headID 进行标识。
在 manager 数组中,每个员工都有一个直属负责人,其中 manager[i] 是第 i 名员工的直属负责人。对于总负责人,manager[headID] = -1。题目保证从属关系可以用树结构显示。
公司总负责人想要向公司所有员工通告一条紧急消息。他将会首先通知他的直属下属们,然后由这些下属通知他们的下属,直到所有的员工都得知这条紧急消息。
第 i 名员工需要 informTime[i] 分钟来通知它的所有直属下属(也就是说在 informTime[i] 分钟后,他的所有直属下属都可以开始传播这一消息)。
返回通知所有员工这一紧急消息所需要的 分钟数 。
示例:
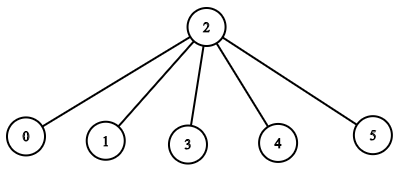
输入:n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0] 输出:1 解释:id = 2 的员工是公司的总负责人,也是其他所有员工的直属负责人,他需要 1 分钟来通知所有员工。 上图显示了公司员工的树结构。
-
思路分析
- 将输入恢复成树结构,每个节点的值就是它传递消息所需的时间。
- 那么问题转化为求和最大的路径。
- DFS。
-
java代码
class Solution { public int numOfMinutes(int n, int headID, int[] manager, int[] informTime) { // 首先用一个map把树恢复出来,key是员工id,value是他的从属id ArrayList<Integer>[] map = new ArrayList[n]; // 遍历manager数组,将每个下属放到他的领导的map中 for (int i = 0; i < n; ++i) { if (manager[i] == -1) { continue; } if (map[manager[i]] == null) { map[manager[i]] = new ArrayList<Integer>(); } map[manager[i]].add(i); } // 从领导开始,分发消息 // 使用深度优先遍历,判断到每一个最后的员工手上最长需要多久 return maxTime(headID, map, informTime); } public int maxTime(int header, ArrayList<Integer>[] map, int[] informTime) { if (map[header]== null) { return 0; } ArrayList<Integer> employees = (ArrayList<Integer>)map[header]; int result = 0; for (int id : employees) { int temp = maxTime(id, map, informTime); result = result > temp ? result : temp; } return result + informTime[header]; } }
4 T 秒后青蛙的位置
-
题目描述
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。 青蛙无法跳回已经访问过的顶点。 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。 无向树的边用数组 edges 描述,其中 edges[i] = [fromi, toi] 意味着存在一条直接连通 fromi 和 toi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。
示例:
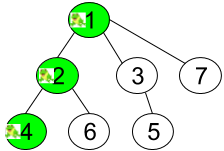
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4 输出:0.16666666666666666 解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。
-
思路分析
- 先将输入恢复成树结构。
- 使用深度优先遍历寻找目标节点,并计算到达目标节点的概率。
- 值得注意的是,题目要求的是
t秒后位于目标顶点上的概率,那么在找到目标节点时,若目标节点不是叶子节点,且t不为0的话,还要继续向下跳,则概率为0。若目标节点是叶子节点,则返回到达此节点的概率。
-
java代码
class Solution { public double frogPosition(int n, int[][] edges, int t, int target) { if (n == 1) { if (target == 1) { return 1.0d; } else { return 0.0d; } } // 还是先把树恢复出来,然后深度优先遍历 ArrayList<Integer>[] tree = new ArrayList[n + 1]; // 为了方便空一个0节点 for (int[] edge : edges) { if (tree[edge[0]] == null) { tree[edge[0]] = new ArrayList<Integer>(); tree[edge[0]].add(0); // 用第0个数作为标记位,记录这个节点是否被访问过。 } if (tree[edge[1]] == null) { tree[edge[1]] = new ArrayList<Integer>(); tree[edge[1]].add(0); } tree[edge[0]].add(edge[1]); tree[edge[1]].add(edge[0]); } return dfs(1, tree, target, t, 1.0d); } public double dfs(int root, ArrayList<Integer>[] tree, int target, int t, double p) { // 如果没有时间了,直接返回 if (t < 0) { return 0.0d; } // 如果这个节点已经来过了 if (tree[root].get(0) == 1) { return 0.0d; } // 如果这个节点就是目标节点 if (root == target) { // 如果此节点就是叶子节点,那么直接返回p if (root != 1 && tree[root].size() == 2) { return p; } else { // 如果此节点有子节点,如果时间恰好是0,返回p if (t == 0) { return p; } else { // 否则,就会往下跳,并且无法返回,返回0 return 0.0d; } } } // 如果这个节点是叶子节点返回0 if (root != 1 && tree[root].size() == 2) { return 0.0d; } // 标记这个节点已经来过 tree[root].set(0, 1); // 计算到达每个子节点的概率 int subNodeNum; // 计算子节点的数量 // 如果是根节点,那么所有与它相连的节点都是他的子节点 if (root == 1) { subNodeNum = tree[root].size() - 1; // -1 去掉头部的标记节点 } else { // 如果不是根节点,那么与他相连的节点中有一个是它的父亲节点 subNodeNum = tree[root].size() - 2; } double averageP = (1.0d / (double)subNodeNum) * p; // 遍历这个节点的所有子节点,如果有一个节点可以跳到target,返回他们跳到target的概率 for (int i = 1; i < tree[root].size(); ++i) { double subP = dfs(tree[root].get(i), tree, target, t - 1, averageP); if (Math.abs(subP - 0.0d) < 0.0000001) { continue; } else { return subP; } } // 退出此节点 tree[root].set(0, 0); return 0.0d; } }