LeetCode第178次周赛题。
1 有多少小于当前数字的数字
-
题目描述
给你一个数组
nums,对于其中每个元素nums[i],请你统计数组中比它小的所有数字的数目。换而言之,对于每个
nums[i]你必须计算出有效的j的数量,其中j满足j != i且nums[j] < nums[i]。以数组形式返回答案。
示例 1:
输入:nums = [8,1,2,2,3] 输出:[4,0,1,1,3] 解释: 对于 nums[0]=8 存在四个比它小的数字:(1,2,2 和 3)。 对于 nums[1]=1 不存在比它小的数字。 对于 nums[2]=2 存在一个比它小的数字:(1)。 对于 nums[3]=2 存在一个比它小的数字:(1)。 对于 nums[4]=3 存在三个比它小的数字:(1,2 和 2)。示例 2:
输入:nums = [6,5,4,8] 输出:[2,1,0,3]示例 3:
输入:nums = [7,7,7,7] 输出:[0,0,0,0] -
思路分析
- 如果使用暴力法,那就是对每个数遍历数组,统计小于它的个数,时间复杂度O(n2)。
- 优化一下,先排序,然后对每个数在排序后的数组中二分查找,查找到位置的位置的下标就是比他小的数字个数。但是数组可能有重复的,所以在查找到下标之后,还要向左移动到它的第一个数才行。
- 时间复杂度:排序O(nlogn),每次查找O(logn),查找n次,总体O(nlogn).
-
Java代码
import java.util.*; class Solution { public int[] smallerNumbersThanCurrent(int[] nums) { int[] result = Arrays.copyOf(nums, nums.length); Arrays.sort(nums); for (int i = 0; i < nums.length; ++i) { int index = Arrays.binarySearch(nums, result[i]); if (index > 0) { // 如果恰好找到这个数,那么就向左遍历,直到它是第一个数 while (index > 0) { if (nums[index - 1] == nums[index]) { --index; } else { break; } } } else { // 应该不存在找不到的情况吧 } result[i] = index; } return result; } }
2 通过投票对团队排名
-
题目描述
现在有一个特殊的排名系统,依据参赛团队在投票人心中的次序进行排名,每个投票者都需要按从高到低的顺序对参与排名的所有团队进行排位。
排名规则如下:
参赛团队的排名次序依照其所获「排位第一」的票的多少决定。如果存在多个团队并列的情况,将继续考虑其「排位第二」的票的数量。以此类推,直到不再存在并列的情况。 如果在考虑完所有投票情况后仍然出现并列现象,则根据团队字母的字母顺序进行排名。 给你一个字符串数组 votes 代表全体投票者给出的排位情况,请你根据上述排名规则对所有参赛团队进行排名。
请你返回能表示按排名系统 排序后 的所有团队排名的字符串。
示例 1:
输入:votes = ["ABC","ACB","ABC","ACB","ACB"] 输出:"ACB" 解释:A 队获得五票「排位第一」,没有其他队获得「排位第一」,所以 A 队排名第一。 B 队获得两票「排位第二」,三票「排位第三」。 C 队获得三票「排位第二」,两票「排位第三」。 由于 C 队「排位第二」的票数较多,所以 C 队排第二,B 队排第三。示例 2:
输入:votes = ["WXYZ","XYZW"] 输出:"XWYZ" 解释:X 队在并列僵局打破后成为排名第一的团队。X 队和 W 队的「排位第一」票数一样,但是 X 队有一票「排位第二」,而 W 没有获得「排位第二」。示例 3:
输入:votes = ["ZMNAGUEDSJYLBOPHRQICWFXTVK"] 输出:"ZMNAGUEDSJYLBOPHRQICWFXTVK" 解释:只有一个投票者,所以排名完全按照他的意愿。示例 4:
输入:votes = ["BCA","CAB","CBA","ABC","ACB","BAC"] 输出:"ABC" 解释: A 队获得两票「排位第一」,两票「排位第二」,两票「排位第三」。 B 队获得两票「排位第一」,两票「排位第二」,两票「排位第三」。 C 队获得两票「排位第一」,两票「排位第二」,两票「排位第三」。 完全并列,所以我们需要按照字母升序排名。示例 5:
输入:votes = ["M","M","M","M"] 输出:"M" 解释:只有 M 队参赛,所以它排名第一。提示:
1 <= votes.length <= 1000 1 <= votes[i].length <= 26 votes[i].length == votes[j].length for 0 <= i, j < votes.length votes[i][j] 是英文 大写 字母 votes[i] 中的所有字母都是唯一的 votes[0] 中出现的所有字母 同样也 出现在 votes[j] 中,其中 1 <= j < votes.length -
思路分析
定义Team类,实现Comparable接口,重写compareTo方法。
-
Java代码
import java.util.Arrays; class Solution { public class Team implements Comparable { public char name = (char)0; public int[] tickets; @Override public int compareTo(Object o) { Team team2 = (Team) o; if (tickets == null) { return 1; } if (team2.tickets == null) { return -1; } for (int i = 0; i < tickets.length; ++i) { if (tickets[i] != team2.tickets[i]) { return team2.tickets[i] - tickets[i]; } } return name - team2.name; } } public String rankTeams(String[] votes) { // 首先创建26个team Team[] teams = new Team[26]; for (int i = 0; i < 26; ++i) { teams[i] = new Team(); teams[i].name = (char)('A' + i); } // 统计票数 for (String voteString : votes) { for (int i = 0; i < voteString.length(); ++i) { char ticket = voteString.charAt(i); // 懒加载 if (teams[ticket - 'A'].tickets == null) { teams[ticket - 'A'].tickets = new int[voteString.length()]; } teams[ticket - 'A'].tickets[i]++; } } // 排名 Arrays.sort(teams); StringBuilder sb = new StringBuilder(); for (Team team : teams) { if (team.tickets != null) { sb = sb.append(team.name); } } return sb.toString(); } }
3 二叉树中的列表
-
题目描述
给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。
如果在二叉树中,存在一条一直向下的路径,且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值,那么请你返回 True ,否则返回 False 。
一直向下的路径的意思是:从树中某个节点开始,一直连续向下的路径。
示例 1:
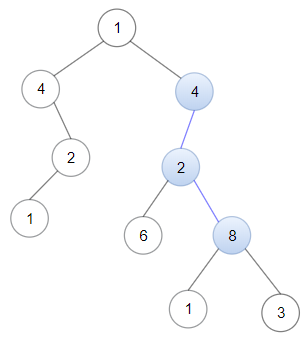
输入:head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3] 输出:true 解释:树中蓝色的节点构成了与链表对应的子路径。 -
思路分析
对二叉树中的每一个节点,求出由此节点出发的每一条路径是否满足要求。
-
Java代码
class Solution { public boolean isSubPath(ListNode head, TreeNode root) { if (head == null) { return true; } if (root == null) { return false; } // 从根节点出发 if (startWith(head, root)) { return true; } else {// 如果不行,分别从左右子节点出发 return isSubPath(head, root.left) || isSubPath(head, root.right); } } public boolean startWith(ListNode head, TreeNode root) { if (head == null) { return true; } if (root == null) { return false; } // 与根节点匹配 if (head.val == root.val) { // 若匹配上,链表的下一个节点再和左右子节点匹配 return startWith(head.next, root.left) || startWith(head.next, root.right); } else { return false; } } }
4 使网络最少有一条有效路径的最小代价
-
题目描述
给你一个 m x n 的网格图 grid 。 grid 中每个格子都有一个数字,对应着从该格子出发下一步走的方向。 grid[i][j] 中的数字可能为以下几种情况:
1 ,下一步往右走,也就是你会从 grid[i][j] 走到 grid[i][j + 1] 2 ,下一步往左走,也就是你会从 grid[i][j] 走到 grid[i][j - 1] 3 ,下一步往下走,也就是你会从 grid[i][j] 走到 grid[i + 1][j] 4 ,下一步往上走,也就是你会从 grid[i][j] 走到 grid[i - 1][j] 注意网格图中可能会有 无效数字 ,因为它们可能指向 grid 以外的区域。
一开始,你会从最左上角的格子 (0,0) 出发。我们定义一条 有效路径 为从格子 (0,0) 出发,每一步都顺着数字对应方向走,最终在最右下角的格子 (m - 1, n - 1) 结束的路径。有效路径 不需要是最短路径 。
你可以花费 cost = 1 的代价修改一个格子中的数字,但每个格子中的数字 只能修改一次 。
请你返回让网格图至少有一条有效路径的最小代价。
示例 1:
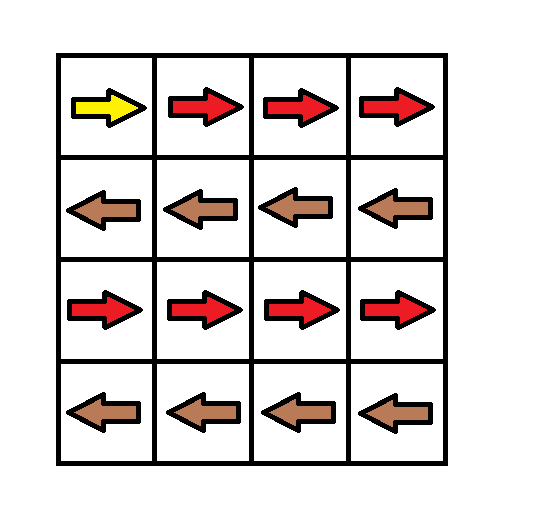
输入:grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]] 输出:3 解释:你将从点 (0, 0) 出发。 到达 (3, 3) 的路径为: (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) 花费代价 cost = 1 使方向向下 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) 花费代价 cost = 1 使方向向下 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) 花费代价 cost = 1 使方向向下 --> (3, 3) 总花费为 cost = 3. -
思路分析
使用广度优先遍历
- 首先,计算改变0次能达到的所有格子。
- 再计算改变1次能达到的所有格子。
- 若达到右下角就返回改变的次数。
- 优化:每次计算改变n次能达到的所有格子时,只从改变n-1次新增的格子出发就可以了。
-
Java代码
/* 使用广度优先遍历,计算改变0次能达到的所有格子,改变1次能达到的所有格子,直到达到右下角就返回 */ class Solution { int rows; int cols; int[][] grid; int[][] arrived; int count; public int minCost(int[][] grid) { rows = grid.length; cols = grid[0].length; this.grid = grid; arrived = new int[rows][cols]; move(0, 0); while (arrived[rows - 1][cols - 1] == 0) { // 遍历上一次新增的所有点,改变它们的方向 ++count; for (int i = 0; i < rows; ++i) { for (int j = 0; j < cols; ++j) { if (arrived[i][j] == count) { // 上一次新增的节点 // 向四个方向分别出发 move(i, j + 1); move(i, j - 1); move(i + 1, j); move(i - 1, j); } } } } return count; } // 从i,j开始移动 public void move(int i, int j) { if (i < 0 || i >= rows || j < 0 || j >= cols) { return; } if (arrived[i][j] != 0) { // 如果这个点已经被到达过了,返回 return; } arrived[i][j] = count + 1;// 表示这个点是在第count次改变时到达的 if (grid[i][j] == 1) { move(i, j + 1); } else if (grid[i][j] == 2) { move(i, j - 1); } else if (grid[i][j] == 3) { move(i + 1, j); } else { move(i - 1, j); } } }