这几题是斐波那契数列和斐波那契数列的变种,也是动态规划类型的题目。
1 斐波那契数列
1.1 题目描述
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。
n<=39
1.2 java代码
/*
第0项为0,第1项为1,后面依次是1、2、3、5、8...(每一项是前两项的和)
*/
public class Solution {
public int Fibonacci(int n) {
if (n <= 1) {
return n;
}
// 只记录前项和前前项,下一项就是这两项的和
int prePre = 0;
int pre = 1;
// 一直计算到第n项为止
for (int i = 2; i <= n; ++i) {
int temp = pre;
pre = pre + prePre;
prePre = temp;
}
return pre;
}
}
2 跳台阶
2.1 题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
2.2 思路
考虑是如何跳上第n阶的,只有两种情况
- 从第n-1阶跳1级上来的
- 从第n-2阶跳2级上来的
那么跳上第n阶的跳法数就是这两种情况的和,第一种情况的跳法数也就是跳上第n-1阶的所有跳法数,第二种情况的跳法数也就是跳上第n-2阶的所有跳法数,也就有:
F(n) = F(n-1) + F(n-2)
这也就是斐波那契数列的递推公式,只不过初始项不同,第一项为1,第二项为2。
2.3 java代码
public class Solution {
public int JumpFloor(int target) {
if (target <= 2) {
return target;
}
// 初始项不同,其他都一样
int prePre = 1;
int pre = 2;
for (int i = 3; i <= target; ++i) {
int temp = pre;
pre += prePre;
prePre = temp;
}
return pre;
}
}
3 变态跳台阶
3.1 题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
3.2 思路
类比上一节的思路有:
F(n) = F(n-1) + F(n-2) + … + F(1) + 1
+1表示从起始点直接跳到第n阶这种跳法。
3.3 java代码
public class Solution {
public int JumpFloorII(int target) {
if (target <= 1) {
return target;
}
// 由于第n阶的跳法数为前面所有阶的跳法数的和,所以用一个数组来记录每一阶的跳法数
int[] dp = new int[target + 1];
// 跳到第[0]阶的跳法是0还是1这个不好讨论,但是由于第n阶还有从起始点直接跳到第n阶这种跳法,所以设置一个dp[0]=1
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= target; ++i) {
dp[i] = 0;
for (int j = 0; j < i; ++j) {
dp[i] += dp[j];
}
}
return dp[target];
}
}
4 矩形覆盖
4.1 题目描述
我们可以用2×1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2×1的小矩形无重叠地覆盖一个2×n的大矩形,总共有多少种方法?
4.2 思路分析
我们考虑矩形的结尾,只有以下两种情况:
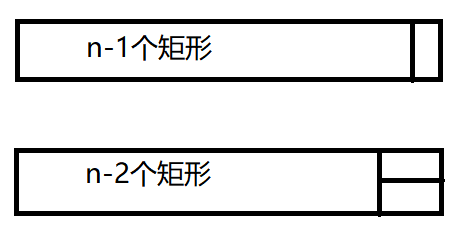
对于任意n个矩形任意摆放,其结尾只有这两种形式,因此,n个矩形的摆放方式总数是这两种结尾的摆放方式的总和。即:
F(n) = F(n-1) + F(n-2)
4.3 java代码
public class Solution {
public int RectCover(int target) {
if (target <= 2) {
return target;
}
// 注意设置初始值
int pre = 2;
int prePre = 1;
for (int i = 3; i <= target; ++i) {
int temp = pre;
pre += prePre;
prePre = temp;
}
return pre;
}
}