1 题目描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
2 思路分析
-
遍历一次肯定能找到结果,时间复杂度为O(n),这题给的数组是有序数组旋转得来的,在有序数组中查找一个数可以用二分查找,时间复杂度为O(logn)。对于这题是不是也可以想办法把时间复杂度降到O(logn)呢?
-
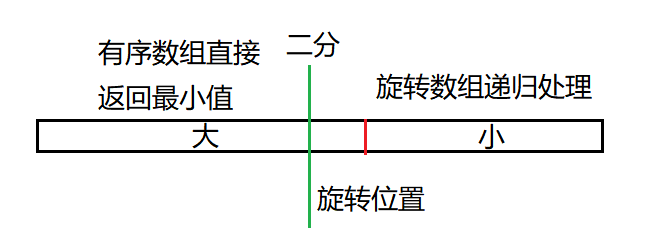
对于有序数组来说,它的最小值就是它的第一个元素,那么我们如果将旋转数组二分的话,很大概率上会得到一个有序数组和一个旋转数组,对于有序数组那一半我们可以直接得到最小值,对于旋转数组那一半就递归解决。这样每次减少一半的情况时间复杂度就是O(logn)。
-
那么怎么判断哪一半是有序数组呢?如果是旋转过的数组,那么第一个元素一定大于等于最后一个元素,反之,如果第一个元素小于最后一个元素就是有序数组了。
3 示例代码
import java.util.ArrayList;
public class Solution {
public int minNumberInRotateArray(int [] array) {
return minNumberInRotateArray1(array, 0, array.length - 1);
}
/*
思路:
遍历一次肯定能找到结果,时间复杂度为O(n),这题给的数组是有序数组旋转得来的,
在有序数组中查找一个数可以用二分查找,时间复杂度为O(logn)。对于这题是不是也可以
想办法把时间复杂度降到O(logn)呢?
对于有序数组来说,它的最小值就是它的第一个元素,那么我们如果将旋转数组二分的话,
很大概率上会得到一个有序数组和一个旋转数组,对于有序数组那一半我们可以直接得到最小值,
对于旋转数组那一半就递归解决。这样每次减少一半的情况时间复杂度就是O(logn)。
那么怎么判断哪一半是有序数组呢?如果是旋转过的数组,那么第一个元素一定大于等于
最后一个元素,反之,如果第一个元素小于最后一个元素就是有序数组了。
*/
public int minNumberInRotateArray1(int [] array, int f, int l) {
// 如果数组只有一个元素,直接返回
if (f == l) {
return array[f];
}
// 如果第一个元素小于最后一个元素,直接返回第一个元素
if (array[f] < array[l]) {
return array[f];
}
// 将数组二分
int mid = (f + l) / 2;
// 递归处理
int leftResult = minNumberInRotateArray1(array, f, mid);
int rightResult = minNumberInRotateArray1(array, mid + 1, l);
// 返回递归结果中较小的那一个
return leftResult < rightResult ? leftResult : rightResult;
}
}